d라이브러리

감기에 걸리지 않으려면 손을 자주 씻고, 얼굴을 만지지 말아야 한다. 호흡기 질환인 감기 바이러스가 손을 타고 얼굴을 거쳐 코나 입으로 전파되기 때문이다. 또 신종플루와 같은 심각한 전염병이 돌면 학교가 쉬고, 환자를 집에서 쉬게 한다. 사람을 통해 전염이 일어나기 때문이다. 이 때 어떤 사람을 쉬게 해야 하고, 어디에 손 소독제를 놓아야 할까? 이런 문제에 가장 효과적인 답을 수학이 갖고 있다.


독감 전염 속도가 더 빨라진 이유
겨울철 사람들이 많이 걸리는 감기의 원인은 주로 바이러스다. 주로 호흡기를 통해 전염되며 손이나 신체 일부의 접촉에 의해서도 옮는다. 접촉성 바이러스는 대개 사람과 사람이 만나야 전염된다.

지난해 개봉된 영화 <;컨테이젼>;은 접촉에 의한 끔찍한 전염병의 공포를 그리고 있다. 영화 속 공포의 원인은 박쥐의 병균이 돼지로 옮아 생긴 치명적 바이러스였다. 이 바이러스는 상상을 초월한 속도로 퍼져 나갔고, 사람들은 손을 쓸 사이도 없이 죽었다.

전염병의 공포는 영화에만 있지 않다. 신종플루, 사스(SARS) 등에 많은 사람들이 감염됐고, 구제역으로 수많은 동물이 죽었다. 실제 1918년에 유행했던 스페인독감으로 인해 2500만~5000만 명이 희생됐다. 미국의 한 신병 훈련소에서 처음 발생한 뒤 1차 세계대전 중 세계 각지로 이동한 군인들에 의해 18개월 만에 세계 인구의 20%가 감염됐고, 그 중 2.5~5%가 사망했다. 이 때는 세계적인 항공망이 제대로 갖춰지기 전이라 전파 속도가 상대적으로 느렸다.

하지만 이젠 누구나 비행기를 타고 세계 어느 곳으로든 하루 안에 이동할 수 있어 전염병이 아주 빠르게 퍼진다. 또한 도시에 사람이 엄청나게 밀집해 있어 전염병이 어떻게 퍼질지 알기 힘들다.

이런 전염병을 막기 위해 오래 전부터 수학을 이용한 연구가 진행됐다.

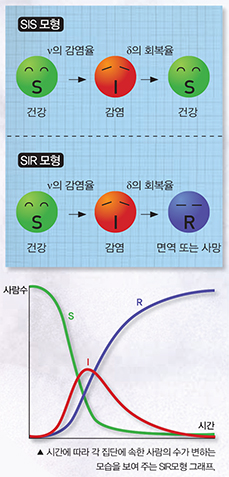
수학적 모형으로 질병 확산을 예측한다

1972년 스코틀랜드의 수학자 윌리엄 컬맥과 예방역학자인 앤더슨 맥켄드릭은 초기 조건과 간단한 모형으로 전염병의 확산을 예측했다. 이들은 우선 사람의 질병 상태를 크게 세 가지로 나눴다. 현재는 감염돼 있지 않지만 면역력이 없어 감염의 가능성이 있는 개체(S), 감염되어 있고 다른 개체를 감염시킬 수 있는 개체(I), 면역력이 있고 건강한 상태에 있는 개체(R)다. 연구자들은 전염의 진행에 따라 세 가지 상태가 어떻게 순환하는지에 관심을 뒀다.

전염확산의 모형은 SIR과 SIS모형 둘로 나뉜다. SIR모형에서 감염된 개체(I)는 υ의 감염률로 이웃한 건강한 개체(S)를 감염키거나, δ의 회복율로 면역력을 가진 건강한 상태(R)가 된다. R 상태의 개체는 더 이상 감염되지도 않고 다른 개체를 전염시킬 수도 없다. 따라서 시간이 충분히 흐른 뒤에는 감염된 개체는 사라지고 S 또는 R만 남는다.

스페인독감이나 천연두 같은 병은 SIR모형에 가깝다. 이들은 감염이 된 뒤 스페인독감처럼 많은 사람이 죽거나, 천연두처럼 병에 걸렸다 나으면 후천적 면역력을 얻어 다시 병에 걸리지 않는다.

반면 SIS모형은 급격히 퍼지거나 완전히 사라지지 않는 평범한 감기 같은 전염병을 설명하는 데 적합하다. 감염된 개체는 υ의 감염률로 이웃한 건강한 개체(S)를 감염시키거나, δ의 회복률로 감염에서 회복된다. SIR모형과 다른 점은 감염된 개체가 회복되었을 때 면역력을 갖는 R 상태가 되는 것이 아니라, 다시 감염이 가능한 S 상태가 되어 전염 확산에 다시 참여할 수 있는 것이다. 감염이 돼도 아주 심각하지 않는 한 죽지 않으며, 면역이 되지 않아 다시 감염될 우려가 있는 질병을 설명한다.


티핑포인트, 독감이 확산될지 가려

복잡계는 네트워크 이론을 바탕으로 물리적, 생물학적, 사회적 대상을 수학적으로 분석한다. 복잡계 연구자들은 전염병 확산 모형을 바탕으로 전염병이 왜 갑작스레 급격히 퍼지는가를 연구했다.

그 결과 회복율과 감염율의 비율에 따라 전염병이 유행하는 정도가 달랐다. 만약 회복율보다 감염율이 높으면 전염병이 널리 퍼지고, 반대로 감염율이 회복율보다 낮으면 전염병이 널리 퍼지지 않는다.

만약 회복율과 감염율이 같다면 전염병은 퍼지지도, 없어지지도 않는 상태로 있게 된다. 이렇게 전염병이 간신히 유지가 되는 지점을 ‘임계점’이라고 한다. 이 임계점을 넘어서면 질병에 걸리는 사람이 폭발적으로 늘어나고, 넘지 못하면 차츰 줄어들다가 결국 사라진다.

임계점을 ‘티핑포인트’라고 부르기도 한다. 널리 퍼지지 않던 전염병이 갑작스럽게 퍼지는 것은 사소한 사건으로 인해 티핑포인트를 넘어섰기 때문이다. 1990년대 중반 미국의 볼티모어에서 매독이란 전염병이 갑자기 빠르게 퍼졌다. 이전에는 매년 조금씩 발생했지만 널리 퍼지지 않았다. 의사들은 지역에서 이 질병을 관리하던 의사의 수가 3분의 1로 줄었으며, 한곳에 모여 살던 감염자들이 이주 정책으로 인해 도시 곳곳으로 퍼져나간 것을 원인으로 찾았다.

하지만 당시엔 이런 설명이 받아들여지지 않았다. 전염병이 퍼지는 원인으로는 너무 사소하다고 생각했기 때문이다.

이에 대해 복잡계 연구자들은 새로운 설명을 내놓았다. 이런 사소한 변화가 임계점 바로 아래 있던 회복율과 감염율의 비율을 임계점 위로 올렸고, 그 결과 전염병이 급격히 확산됐다는 것이다.


마당발 막아 전염병 막는다

그렇다면 이런 전염병을 막기 위해선 어떻게 해야 할까. 복잡계 연구자들은 점과 선으로 된 그래프로 질병의 확산과정을 그렸다. 이 때 사람은 점이고, 두 점 사이에 전염병이 퍼지면 선으로 연결했다. 그러자 전염병을 많이 퍼트리는 사람이 드러났다. 우리 주변에 있는 마당발(허브)과 같이 아는 사람이 많은 사람이었다. 실제로 미국에서 지방 소도시의 전염병이 퍼지는 과정을 연구한 결과 택배를 배달하는 사람이 허브 역할을 했다. 이 사람은 우편물을 배달하며 많은 사람을 만나기 때문에 병에 걸릴 확률도 높고, 병에 걸린 뒤 많은 이웃에게 병을 퍼트렸다. 이런 허브가 많으면 많을수록 전염병을 막기가 힘들다.

이런 연구를 통해 허브가 병에 걸리지 않도록 막으면 된다는 것이 밝혀졌다. 전염병이 급격하게 퍼지더라도 모든 사람을 격리시키거나 예방접종을 할 수는 없다. 또 아무나 골라 예방접종을 하는 것은 효과가 떨어진다. 따라서 허브를 골라 먼저 접종하면 전염병이 퍼지는 걸 막을 수 있다.

또한 감염되는 경로를 추적해 서로 만나는 고리를 끊을 수도 있다.

무심코 만지는 종이, 택배, 버스·지하철의 손잡이에 묻은 바이러스는 길게는 며칠 동안 살아 있다. 따라서 손을 자주 씻으면 전염되는 연결고리를 끊을 수 있다.

더 나아가 각 도시별 항공편수와 승객수를 통계분석해 사스와 신종플루의 전염지역이나 환자수를 어느 정도 예측할 수 있다. 그리고 이를 바탕으로 격리 조치나 백신 접종을 하면 큰 효과를 거둘 수 있다.


전염병 네트워크로 인터넷과 생명 연구

구글은 전염병의 관계망을 파악했던 방식과 같이 네트워크의 구조를 파악해 조금 더 좋은 검색엔진을 만들었다. 구글이 나오기 전까지 검색 시장에서 야후가 앞서 있었다. 야후는 여러 웹 페이지를 범주별로 분류해 보여 주는 방식이어서, 인터넷에서의 웹페이지가 폭발적으로 늘어나자 일일이 범주를 정해 분류하기가 힘들었다.

구글은 사람들이 많이 찾는 웹페이지(허브)가 처음에 나오도록 컴퓨터가 알아서 보여 주는 검색엔진을 만들어 야후를 제쳤다.

정하웅 KAIST 물리학과 교수는 작년 10월 26일 치러진 서울시장 보궐선거 전날, 구글의 검색 원리를 이용해 선거 결과를 예측했다.

박원순 후보와 나경원 후보를 구글에서 검색해 각각의 웹페이지 수를 뽑은 결과가 실제 득표율과 비슷했던 것이다. 사람들의 관심과 지지도가 인터넷의 웹페이지 수에 반영됐기 때문이다. 이뿐만 아니라 2007년 우리나라 대통령 선거와 2008년 미국 대통령 선거에서도 구글 검색 결과와 득표율이 비슷했다. 이 밖에도 네트워크 연구를 바탕으로 새로운 학문인 시스템생물학*이 탄생하기도 했다.

독감이나 신종플루가 퍼질 때 학교에 나오지 못하게 하고, 손을 자주 씻게 한 것은 수학적 이유가 있다. 평소 활발한 인간관계를 자랑하는 마당발이라면 독감에 걸렸을 때 활동을 줄이는 것이 친구를 위한 일일 수도 있다.